Difference between revisions of "Monitor and operate the microwaves / know how to find correct frequency"
| Line 13: | Line 13: | ||
In order to find both the ideal mm-wave and NMR frequencies, some combination of the above numbers are multiplied by the magnetic field strength <math>B</math> in T. This gives the particle's Larmor frequency, <math>\nu_i = \frac{\gamma_i}{2\pi}B</math>, that is used in the descriptions below. | In order to find both the ideal mm-wave and NMR frequencies, some combination of the above numbers are multiplied by the magnetic field strength <math>B</math> in T. This gives the particle's Larmor frequency, <math>\nu_i = \frac{\gamma_i}{2\pi}B</math>, that is used in the descriptions below. | ||
| − | ==Proton | + | ==Proton Enhancement== |
| + | |||
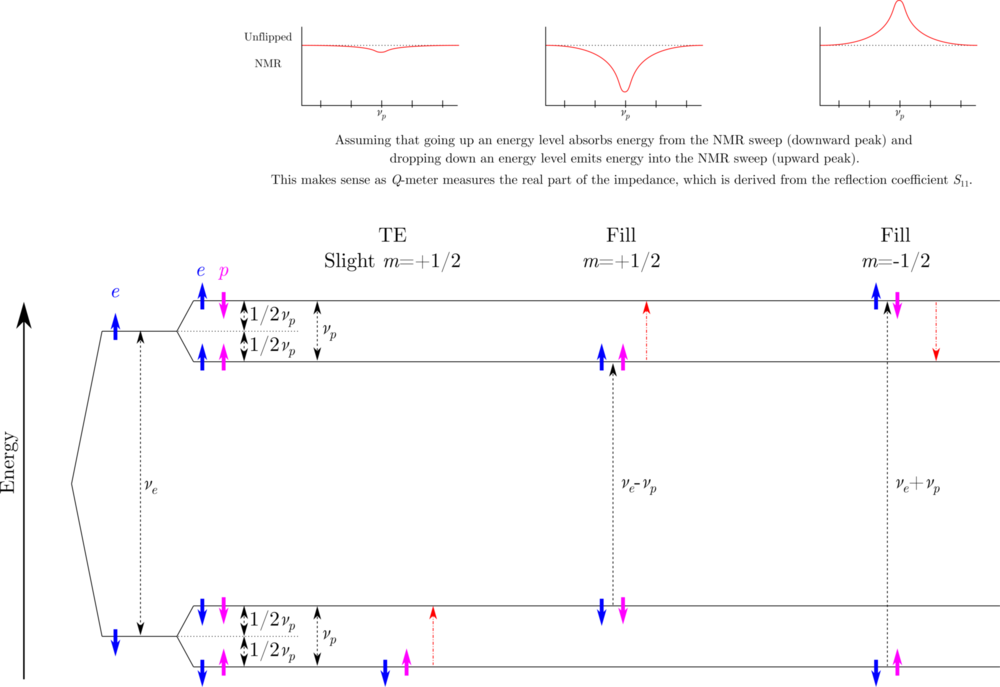
| + | The image below shows the energy level splitting of the proton, along with the expected NMR spectra along the top. These energy splittings are a useful guide for determining a good initial estimate of the polarization enhancement frequency for the mm-waves. | ||
[[File:proton_mmwaves.png|1000px]] | [[File:proton_mmwaves.png|1000px]] | ||
| Line 34: | Line 36: | ||
## Carefully go down in frequency to see if the maximum polarization improves | ## Carefully go down in frequency to see if the maximum polarization improves | ||
# Keep track of where maximum polarization occurred and use that as your frequency | # Keep track of where maximum polarization occurred and use that as your frequency | ||
| + | |||
| + | ==Deuteron Enhancement== | ||
| + | |||
| + | Due to a combination of the additional spin-0 state and energy-level shifts due to quadrupole effects in nuclei such as ND<sub>3</sub>, find ideal frequencies is much more complicated than it is for the proton. However, the same basic procedure can be followed using energy level diagrams as a guide. | ||
Revision as of 17:50, 12 June 2020
Using LabView for mmWaves
- (David?)
Finding the correct frequency
In order to start looking for the optimum millimeter/microwave frequency, the variables below are important to know. Note that here the frequencies are given in GHz for finding mmwave frequency, as the frequency for 5 T fields will always be around 140 GHz, and in MHz for nuclei to aid in finding NMR signals.
- Electron Gyromagnetic Ratio: <math>\frac{\gamma_e}{2\pi}=28.024~951~6~\mathrm{GHz/T}</math>
- Proton Gyromagnetic Ratio: <math>\frac{\gamma_p}{2\pi}=0.042~577~478~92~\mathrm{GHz/T}=42.577~478~92~\mathrm{MHz/T}</math>
- Deuteron Gyromagnetic Ratio: <math>\frac{\gamma_D}{2\pi}=0.006~535~902~311~\mathrm{GHz/T}=6.535~902~311~\mathrm{MHz/T}</math>
In order to find both the ideal mm-wave and NMR frequencies, some combination of the above numbers are multiplied by the magnetic field strength <math>B</math> in T. This gives the particle's Larmor frequency, <math>\nu_i = \frac{\gamma_i}{2\pi}B</math>, that is used in the descriptions below.
Proton Enhancement
The image below shows the energy level splitting of the proton, along with the expected NMR spectra along the top. These energy splittings are a useful guide for determining a good initial estimate of the polarization enhancement frequency for the mm-waves.
- Find & measure TE using the Larmor Frequency
- <math> \nu_p = \frac{\gamma_p}{2/pi}B</math>
- Use the central value of the measured TE to extract the magnetic field for the calculations below
- <math> \nu_p = \frac{\gamma_p}{2/pi}B</math>
- To calculate the best positive enhancement frequency for mm-waves:
- <math>f_{\uparrow}=\nu_e-\nu_p</math>
- To calculate the best negative enhancement frequency for mm-waves:
- <math>f_{\downarrow}=\nu_e+\nu_p</math>
Note that the above should be considered starting points. The actual frequency will shift slightly due to the number and position of free radicals in the material (this causes <math>\nu_e</math> to shift slightly). It's good practice to:
- Start at the frequencies calculated above
- Carefully go up in frequency and note if the maximum polarization increases or decreases
- Typically the above calculations tend to be slightly lower than the actual polarization numbers, though this may not always be the case
- If a point of maximum polarization is not found:
- Go back to the starting frequency
- Carefully go down in frequency to see if the maximum polarization improves
- Keep track of where maximum polarization occurred and use that as your frequency
Deuteron Enhancement
Due to a combination of the additional spin-0 state and energy-level shifts due to quadrupole effects in nuclei such as ND3, find ideal frequencies is much more complicated than it is for the proton. However, the same basic procedure can be followed using energy level diagrams as a guide.