Lecture 4 - Transverse Waves Part III.
We finish Chapter 17 and start 18.
![]()
Interference
When 2 waves interfere we can use the principle of superposition to add up the resulting waves:
|
|
(1.1) |
For the special case of two sine waves that travel in the
same direction, with the same frequency, the same wavelength and the same
amplitude, but a different phase, this result simplifies. Using the trig
formula: for two waves, we get:
|
|
(1.2) |
(Note that it does not make a difference whether and
or the other way around, since cos(x)=cos(-x) )
In equation 1.2, the red part is the new amplitude, and the blue part the new oscillating term.
Phasors
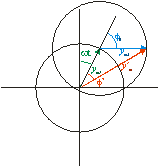 When
the two waves on a string do not have the same amplitude we can still add them.
In fact we can add any two waves using equation 1.1. One trick for adding two
waves with the same frequency and wavelength is a phasor diagram. Because of
the sine term, the displacement of a wave can be seen as the y component of a
vector that is rotating with an angular velocity
When
the two waves on a string do not have the same amplitude we can still add them.
In fact we can add any two waves using equation 1.1. One trick for adding two
waves with the same frequency and wavelength is a phasor diagram. Because of
the sine term, the displacement of a wave can be seen as the y component of a
vector that is rotating with an angular velocity .
Two waves can then be added as two vectors, which is easier than two sine
terms. It is far easier to add two vectors and then look at the resulting
vector’s angle and y component than it is do the math for the sum of two sine
term.
Standing Waves
When two waves travel in the opposite direction of each other we can still perform the same trick as equation 1.2, except that the term arrange themselves slightly differently:
|
|
(1.3) |
Note that really just the term “hopped” from the sin to the cos term.
The result is a very different wave though!
Note that since the term is gone, the resulting wave not longer
appears to travel. The blue part equation 1.3 gives the shape of the wave with
respect to x. This shape means that
the amplitude of the oscillations (with frequency
) of each element of the string changes with
position. Another way to look at the
same thing is that the blue part defines a shape with respect to x and the green part causes the
amplitude of this shape to change with time.
Such a wave is called a standing wave.
Properties of a standing wave.
The locations along x
where the nodes occur (the point
where the amplitude is zero) are found when the term is equal to zero, thus, with n=0,1,2,…
|
|
(1.4) |
Note that the book sets the phase term equal to zero, which simplifies the equation. We can always find a clever location for the origin (i.e. at a node) so that we do not need the phase factor.
Similarly, we can find the maxima, which results in:
|
|
(1.5) |
Trick question: What happens with the energy in a standing wave? Does it still get transported like it does in a traveling wave?
Reflections at the end of a string.
When a wave hits the end of a string, which is clamped down
(fixed) this wave can not travel any further. The energy can not travel any
further either, since the point can not do any work
( ,
and
is zero). The only option for this energy is
to reflect back, which is what it does. The wave will invert itself, and travel
back where it came from. It is inverted, so that the fixed point can act as a
node.
When the same thing happens on a loose end (a ring sliding
on a rod), the energy can not go further either. There is a ,
but now there is no F. The wave is
reflected back without inverting.
Standing Waves and Resonance
An ideal string clamped between to fixed points can have a wave on it that continuously reflects back and forth. (If the string is not ideal, the wave will damp out, and we would somehow need to add some energy to keep it going.) For certain frequencies, called resonant frequencies, all these reflecting overlapping waves will perfectly add up to one large standing wave. For off resonant frequencies they will tend to cancel each other out.
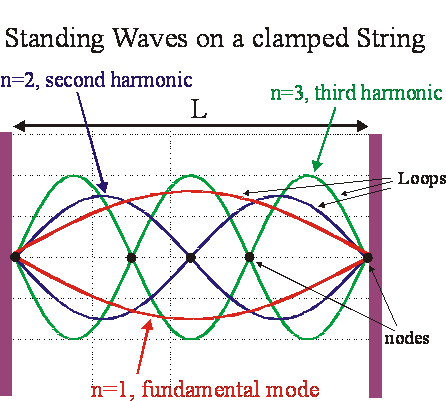
The lowest frequency for which such a standing wave occurs,
the fundamental mode, would have
exactly one half wavelength between the two clamped points: .
The next one up would have 1 wavelength, the next one 1.5 etc. So:
|
|
(1.6) |
Or using we can write:
|
|
(1.7) |
When n=1 we talk of the fundamental mode or the first harmonic, with n=2 we get the second harmonic etc. Sometimes n is called the harmonic number.
Since we count the nodes at the end, the first harmonic has 2 nodes, one loop. The second harmonic has 3 nodes and 2 loops, etc.
Sound Waves
Sound is a longitudinal wave that travels through a material in the form of small compressions and expansion, along the direction of travel of the wave.
Speed of Sound
To get to the speed of sound, we first need to know something about the compressibility of the the material the sound travels through. This is given by the amount of pressure that is created when a certain volume is compressed a little bit. The quantity is called the bulk modulus and comes from the equation:
|
|
(1.8) |
the speed of sound is then given by:
|
|
(1.9) |
where is the density of the medium. The speed of
sound in air is between 331 (at 0 C) and 343 m/s (at 20C).